Непрекъснатост
Терминът spline, в сферата на компютърните науки CAD (Computer-Aided Design) и компютърната графика, много често се отнася към частично-параметричната полиномиална крива. Сплайновете (splines) са популярен начин за представяне на криви в тази област, поради простотата на тяхната конструкция, тяхното удобство и точност на оценката, както и поради възможността им да изобразяват сложни форми чрез приспособяване на крива и интерактивен дизайн на кривата. Терминът сплайн (spline) идва от пластичните сплайн устройства, използвани от корабосторителите и чертожниците за чертане на плавни форми.
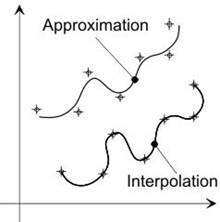
Когато се правят настройки на кривата, се използват контролни точки и, в зависимост от кривата, се определя финалната крива, дали минава през контролните точки (интерполира) или близко до тях (доближава).
Зад кривите седи една доста сложна математическа теория. Всяка крива или част от нея са описани от някакво математическо уравнение. Кривите се моделират чрез контролни точки и техният брой е стриктно свързан с математическия модел на кривата. Проблемът е, че когато се моделира много сложна крива, са необходими голям брой точки (да кажем 20). Но това води до полиномна крива с порядък 19 и е много трудно да се работи с нея, пресмята се и се рендира бавно. Този проблем е решен чрез сегменти. Кривата е съставена от няколко по-къси части, наречени сегменти. Когато се използват четири контролни точки за моделиране на един сегмент, говорим за кубична крива.

Непрекъснатостта е особеност на кривата, използвана в математическата теория на кривите, която показва как се държи кривата при свръзките. Кривите са съставени от сегменти и непрекъснатостта във връзката на сегментите е критичен фактор. Сегментът (кубична крива) се нуждае от четири зададени контролни точки, за да може самият той да се моделира.
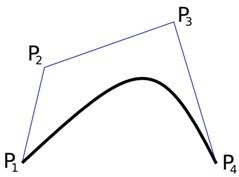
Разполагайки със сегменти, те могат да бъдат използвани, за да се свържат в крива с различна непрекъснатост. Има няколко вида непрекъснатост:
- Тъждественост на последователни крайни точки,
- Тъждественост на тангециални вектори в последователни крайни точки,
- Тъждественост на вторите производни вектори в последователни крайни точки, и т.н

Плавността на кривите при връзките зависи от вида непрекъснатост. Най-високият клас непрекъснатост има най-добра гладкост при най-високо отклонение. Това означава, че при използването на сплайн като траектория за анимация, обектът минаващ по протежението на траекторията няма рязко да промени неговата скорост при двете връзки на сегментите.