Доближаващи (Approximation) криви
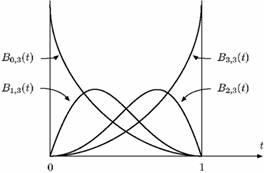
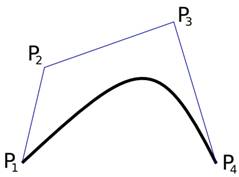
Доближаващите криви не минават през контролните точки, но са привлечени от тях. Разстоянието на кривата от контролните точки зависи от особеностите на кривата. В математиката кривата на Bezier е параметрична крива, важна за компютърната графика. Кривата на Bezier се представя чрез полиномиали на Bernstein (Bernstein polynomials) (виж фиг.35 вляво), която има много интересни характеристики: положителни стойности, сумиране към едно, обратни полиномни определения, лесно достигане на добра непрекъснатост.
|
|
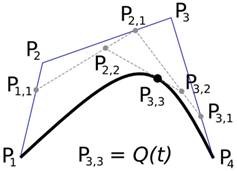
Полиномите на Bernstein прехвърлят влиянието на контролните точки към крайната доближаваща крива на Bezier. Числено устойчив метод за пресмятане на кривата на Bezier е алгоритъмът на de Casteljau's, използвайки рекурсивни алгоритми, базирани на обратното полиномно определение на Bernstein. Алгоритъмът е много полезен при растеризацията на криви.
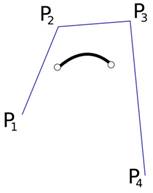
B-spline, друг вид доближаваща крива, е обобщение на кривата на Bezier, съставена от непрекъснати свързани сегменти от кубични криви на Coons. Предимството е в промените на кривата, предизвикани от контролните точки, или промените в параметрите са само локални. Само сегментите, които са близко до промените, са преизчислени. По-нататъшното обобщение води до NURBS.
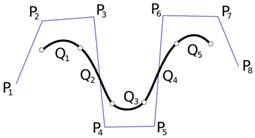
NURBS, съкращение за непостоянен, рационален B-spline, е математически модел, използван основно в компютърната графика за генериране и представяне на криви и повърхности. Кривата NURBS се определя от нейната последователност, настройка на тежест на контролните точки и векторни възли. Кривите и повърхностите NURBS са обобщение и на кривите и повърхностите от типа B-spline и от типа Bezier, основната разлика е в тежестта на контролните точки, което прави кривите NURBS рационални. Контролните точки при кривите на Bezier имат тежест 1.0 (нерационално), обратно на NURBS. Премереността на контролните точки оказва влияние върху това, как контролните точки притеглят финалната крива.
Новият параметър, векторнитя възел, оказва влияние върху параметричната дължина на сегментите на кривата. Всеки сегмент е проста крива (кубична), която е функция от някакъв параметър. В тази връзка, параметричната дължина на един сегмент е 1 (първата точка от сегмента на кривата е с параметър 0, а последната с 1). Това е еднородност на кривата. Но NURBS не са еднородни, сегментите не са с една и съща параметрична дължина.
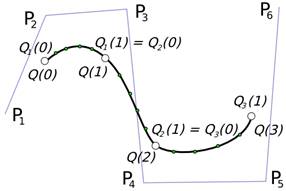
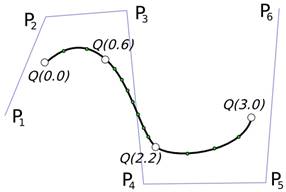
Твърдението, че кривите NURBS обобщават кривите на Bezier, означава че всички криви на Bezier са криви NURBS, но не всички криви NURBS са криви на Bezier. Обобщението често означава, че такъв модел е много по-силен в моделирането и възможността за описване, но по-малко ефективен и скъп в изчислително отношение.