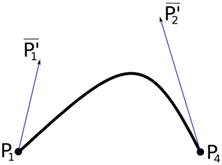
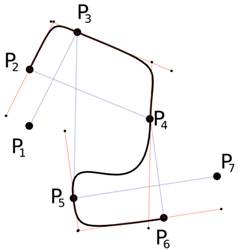
Интерполационни криви
Кубичните криви на Ferguson е най-разпространената интерполационна крива, контролирана от две крайни точки и два тангенциални вектора (виж фиг.39, ляво). Непрекъснатостта е постигната чрез тъждество на крайните точки и тангенциалните вектори от последващите сегменти. Оформянето на кривите е твърде неинтуитивно и не е интерактивно.
Друга интерполационна крива е сплайна на Kochanek-Bartels, използващ кубичните криви на Ferguson, която намира приложение най-вече при анимацията. Кривата се контролира също така и от други параметри, като опъване, скосеност, и непрекъснатост, определяща поведението на промените на тангентите (допирателните).
Сплайнът Catmull-Rom (виж фиг. 39, дясно) е друг вид интерполационна крива, базирана на сплайна на Hermite, чиито допирателни се определят от точките и параметъра на опъване със стойност 0,5. На схемата, която показва строежа на една крива (фиг. 39, дясно), е изобразено, как съседните контролни точки оказват влияние на тангенционалните вектори.
|
|